La integración es un concepto fundamental del cálculo y del análisis matemático. Básicamente, una integral es una generalización de la suma de infinitos sumandos, infinitamente pequeños.
El cálculo integral, encuadrado en el cálculo infinitesimal, es una rama de las matemáticas en el proceso de integración o antiderivación. Es muy común en la ingeniería y en la ciencia; se utiliza principalmente para el cálculo de áreas y volúmenes de regiones y sólidos de revolución.
Fue usado por primera vez por científicos como Arquímedes, René Descartes, Isaac Newton, Gottfried Leibniz e Isaac Barrow. Los trabajos de este último y los aportes de Newton generaron el teorema fundamental del cálculo integral, que propone que la derivación y la integración son procesos inversos.
Principales objetivos del cálculo integral
Sus principales objetivos a estudiar son:
- Área de una región plana
- Cambio de variableIntegrales indefinidas
- Integrales definidas
- Integrales impropias
- Integral de línea
- Integrales múltiples (dobles o triples)
- Integrales trigonométricas, logarítmicas y exponenciales
- Métodos de integración
- Teorema fundamental del cálculo
- Volumen de un sólido de revolución

Teoría
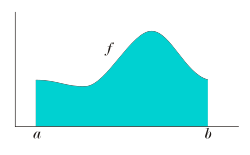
Dada una función de una variable real y un intervalo de la recta real, la integral es igual al área de la región del plano limitada entre la gráfica de , el eje , y las líneas verticales y , donde son negativas las áreas por debajo del eje .
La palabra "integral" también puede hacer referencia a la noción de primitiva: una función F, cuya derivada es la función dada . En este caso se denomina integral indefinida, mientras que las integrales tratadas en este artículo son las integrales definidas. Algunos autores mantienen una distinción entre integrales primitivas e indefinidas.
Los principios de la integración fueron formulados por Newton y Leibniz a finales del siglo XVII. A través del teorema fundamental del cálculo, que desarrollaron los dos de forma independiente, la integración se conecta con la derivación, y la integral definida de una función se puede calcular fácilmente una vez se conoce una antiderivada. Las integrales y las derivadas pasaron a ser herramientas básicas del cálculo, con numerosas aplicaciones en ciencia e ingeniería.
Bernhard Riemann dio una definición rigurosa de la integral. Se basa en un límite que aproxima el área de una región curvilínea a base de partirla en pequeños trozos verticales. A comienzos del siglo XIX, empezaron a aparecer nociones más sofisticadas de la integral, donde se han generalizado los tipos de las funciones y los dominios sobre los cuales se hace la integración. La integral curvilínea se define para funciones vectoriales de una variable, y el intervalo de integración [a,b] se sustituye por el de la parametrización de la curva sobre la cual se está integrando, la cual, conecta dos puntos del plano o del espacio. En una integral de superficie, la curva se sustituye por un trozo de una superficie en el espacio tridimensional.
Las integrales de las formas diferenciales desempeñan un papel fundamental en la geometría diferencial moderna. Estas generalizaciones de la integral surgieron primero a partir de las necesidades de la física, y tienen un papel importante en la formulación de muchas leyes físicas cómo, por ejemplo, las del electromagnetismo. Los conceptos modernos de integración se basan en la teoría matemática abstracta conocida como integral de Lebesgue, que fue desarrollada por Henri Lebesgue.
Propiedades de la integración
Linealidad
- El conjunto de las funciones Riemann integrables en un intervalo cerrado [a, b] forman un espacio vectorial con las operaciones de suma (la función suma de otras dos es la función que a cada punto le hace corresponder la suma de las imágenes de este punto por cada una de las otras dos) y la multiplicación por un escalar. La operación integración
-
- es un funcional lineal de este espacio vectorial. Así, en primer lugar, el conjunto de funciones integrables es cerrado con la combinación lineal, y en segundo lugar, la integral de una combinación lineal es la combinación lineal de las integrales,
-
- De forma parecida, el conjunto de las funciones reales Lebesgue integrables en un espacio métrico E dado, con la medida μ es cerrado respecto de las combinaciones lineales y por lo tanto forman un espacio vectorial, y la integral de Lebesgue
-
- es un funcional lineal de este espacio vectorial, de forma que
-
- De forma más general, si se toma el espacio vectorial de todas las funciones medibles sobre un espacio métrico (E,μ), que toman valores en un espacio vectorial topológico completo localmente compacto V sobre un campo topológico localmente compacto K, f : E → V. Entonces se puede definir una aplicación integración abstracta que a cada función f le asigna un elemento de V o el símbolo ∞,
-
- que es compatible con las combinaciones lineales. En esta situación, la linealidad se sostiene para el subespacio de las funciones, cuya integral es un elemento de V (es decir, las integrales "finitas"). Los casos más importantes surgen cuando K es R, C, o una extensión finita del campo Qp de números p-ádicos, y V es un espacio vectorial de dimensión finita sobre K, y cuando K=C y V es un espacio de Hilbert complejo.
La linealidad, junto con algunas propiedad naturales de continuidad y la normalización para ciertas clases de funciones "simples", se pueden usar para dar una definición alternativa de integral. Este es el enfoque de Daniell para el caso de funciones reales en un conjunto X, generalizado por Bourbaki a funciones que toman valores en un espacio vectorial topológicamente compacto. Véase Hildebrandt (1953)11 para una caracterización axiomática de la integral.
Desigualdades con integrales
Se verifican varias desigualdades generales para funciones Riemann integrables definidas en un intervalo cerrado y acotado [a, b] y se pueden generalizar a otras nociones de integral (Lebesgue y Daniell).
- Cotas superiores e inferiores. Una función f integrable en [a, b], es necesariamente acotada en el intervalo. Por lo tanto hay dos números reales m y M tales que m ≤ f (x) ≤ M para todo x de [a, b]. Dado que los sumatorios superior e inferior de f sobre [a, b] son también acotados para m(b − a) y M(b − a) respectivamente, de aquí resulta que
-
- Desigualdades entre funciones. Si f(x) ≤ g(x) para todo x de [a, b] entonces cada uno de los sumatorios superior e inferior de f son acotados inferior y superiormente por los sumatorios superior e inferior de g respectivamente. Así
-
- Esto es una generalización de las desigualdades anteriores, dado que M '(b − a) es la integral de la función constante con valor M en el intervalo [a, b].
- Subintervalos. Si [c, d] es un subintervalo de [a, b] y f(x) es no negativa para todo x, entonces
-
- Productos y valores absolutos de funciones. Si f y g son dos funciones, entonces podemos emplear su producto, potencias y valores absolutos:
-
- Si f es Riemann integrable en [a, b] entonces lo mismo se cumple para |f|, y
- Es más, si f y g son ambas Riemann integrables entonces f 2, g 2, y fg son también Riemann integrables, y
- Esta desigualdad se conoce como desigualdad de Cauchy-Schwarz, y desempeña un papel fundamental en la teoría de los espacios de Hilbert, donde el lado de la derecha se interpreta como el producto escalar de dos funciones integrables f y g en el intervalo [a, b].
- Desigualdad de Hölder. Si p y q son dos números reales, 1 ≤ p, q ≤ ∞ con 1/p + 1/q = 1, y f y g son dos funciones Riemann integrables. Entonces las funciones |f|p y |g|q también son integrables y se cumple la desigualdad de Hölder:
- Para el caso de p = q = 2, la desigualdad de Hölder pasa a ser la desigualdad de Cauchy–Schwarz.
- Desigualdad de Minkowski. Si p ≥ 1 es un número real y f y g son funciones Riemann integrables. Entonces |f|p, |g|p y |f + g|p son también Riemann integrables y se cumple la desigualdad de Minkowski:
- Una desigualdad análoga a ésta para la integral de Lebesgue se usa en la construcción de los espacios Lp.
Convenciones
sobre un intervalo [a, b] está definida si a < b. Esto significa que los sumatorios superiores e inferiores de la función f se evalúan sobre una partición a = x0 ≤ x1 ≤ . . . ≤ xn = b cuyos valores xi son crecientes. Geométricamente significa que la integración tiene lugar "de izquierda a derecha", evaluando fdentro de intervalos [x i , x i +1] donde el intervalo con un índice más grande queda a la derecha del intervalo con un índice más pequeño. Los valores a y b, los puntos extremos del intervalo, se denominan límites de integración de f. Las integrales también se pueden definir si a > b:
- Inversión de los límites de integración. si a > b entonces se define
-
Ello, con a = b, implica:
- Integrales sobre intervalos de longitud cero. si a es un número real entonces
-
La primera convención es necesaria al calcular integrales sobre subintervalos de [a, b]; la segunda dice que una integral sobre un intervalo degenerado, o un punto, tiene que ser cero. Un motivo para la primera convención es que la integrabilidad de f sobre un intervalo [a, b] implica que f es integrable sobre cualquier subintervalo [c, d], pero en particular las integrales tienen la propiedad de que:
- Aditividad de la integración sobre intervalos. si c es cualquier elemento de [a, b], entonces
-
Con la primera convención la relación resultante
queda bien definida para cualquier permutación cíclica de a, b, y c.
En lugar de ver lo anterior como convenciones, también se puede adoptar el punto de vista de que la integración se hace solo sobre variedades orientadas. Si M es una tal forma m-dimensional orientada, y M' es la misma forma con orientación opuesta y ω es una m-forma, entonces se tiene (véase más abajo la integración de formas diferenciales):






![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)

























No hay comentarios:
Publicar un comentario