¿Qué problemas internos están pasando dentro de la
cúpula?
Desde días atrás tras el oficialismo ganar la
mayoría de las gobernaciones del pueblo venezolano, la ANC de forma casi
inmediata colocó fecha para el 10 de Diciembre del año en curso las elecciones
de alcaldes. De esta forma la cúpula del PSUV anunció sus candidatos a dedo ya
que no realizó primarias para definir los mismos.
¿Qué división política e interna ocasionó esto?
Muchos de los que querían ser partícipes en estas elecciones como candidatos quedaron por fuera, después que
hasta había pateado las calles y se habían dado a conocer por su pueblo para
dichas elecciones. Siendo este el motivo por el cual muchos decidieron optar
por otros partidos y otros por un partido independiente, luego de buscar e
indagar en que otros partidos se habían postulado el régimen también les quita
las candidaturas por negociaciones con el PSUV, apoyando entonces los otros
partidos de izquierda al PSUV y dejando nuevamente por fuera a los que querían
participar.
¡Ahora viene lo bueno!
|
Revolución dentro de la revolución, el partido
TUPAMARO decidió no apoyar a todos los candidatos de todos los municipios,
salió al ruedo con 21 candidatos a alcaldías en diferentes estados del país,
TUPAMARO siendo un partido que apoyó a Hugo Chávez y ahora a Nicolas Maduro
decidió lanzarse a la calle exigiéndole al presidente Nicolas Maduro el apoyo
en estas candidaturas y Nicolas sin poder hacer nada accedió a esto y le
quitó la tarjeta del PSUV a 21 candidatos que ya había impuesto, dándole así
la tarjeta del PSUV a estos 21 candidatos TUPAMARO a nivel nacional.
|
|
¿Descontento político y social por parte de sus
seguidores?
Así es, muchos de sus seguidores han dicho que no
saldrán a votar por candidatos TUPAMARO, que les parece eso una falta de
respeto hacia el pueblo que apoya al PSUV, que además luego de imponer los
candidatos en su partido, ahora le imponen uno de otro partido.
¿Qué será lo que le avecina al pueblo venezolano
tras estas elecciones? Seguiremos informando...
|
|














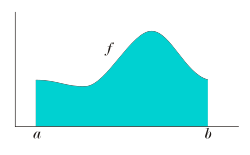



![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
























